Came across an interesting video from one of the users of Perl: Is Perl dead? @Randal L. Schwartz on Dart and Flutter @Code Maven

Strictly speaking not news exactly, given that it dates from early 2018, but it was news to me, and since I haven’t seen it make the rounds I still find it worth disseminating. From the MySQL 8.0.11 release notes:

The utf8mb3 character set will be replaced by utf8mb4 in a future MySQL version. The utf8 character set is currently an alias for utf8mb3, but will at that point become a reference to utf8mb4. To avoid ambiguity about the meaning of utf8, consider specifying utf8mb4 explicitly for character set references instead of utf8.

This a declaration of intent rather than a change that has happened… but still. It’s been a very long September…

(To prepare for this you’ll want to note what you need to take into account regarding the way utf8mb4 and indexes interact.)

In which we leap tall primes in a single bound, mis-take a tree, test percussion, and find the limits of a Curious Module.

Task 1: 10001st Prime Number - One-liners (expanded) in Raku and Perl.

Task 2: Curious Fraction Tree - Solutions in Raku and Perl (with 200+ tests), and another Perl solution using a CPAN module.

TWC Task #1, 10001st Prime Number

Perl

My Perl program is a 3-line version of this one-liner:

perl -Mntheory=nth_prime -wE 'say nth_prime(10_001)'

The ntheory (Number Theory) module has many routines that would solve the problem. nth_prime is the most direct.

Raku

constant @primes = (2, 3, 5, 7 ... *).grep(&is-prime);
say @primes.skip(10_000).head;

That first line creates a "constant" lazy infinte array of primes. It is constant in the sense that the program code cannot alter a value, but it is lazy, so the elements of @primes[0..N] are not generated until something tries to use @primes[N]. All the prior elements are cached and delivered on request without recalculation. If a higher element is requested later in the program's execution, then the generation of @primes elements will resume where it left off.

TWC Task #2, Curious Fraction Tree

I studied the patterns of parent->children and child->parent, slung some code to solve the task, wrote more to extend the tree, and searched OEIS and the Web.

Observations:

• The "Curious Fraction Tree" is properly named the "Calkin-Wilf Tree", but is easily confused with the 150+year-earlier "Stern-Brocot tree".
  (by "easily confused", I mean that I confused them. Also confused C-W with Kepler's tree of harmonic fractions.)

• Coolest illustration of the C-W tree: https://www.jasondavies.com/calkin-wilf-tree/

• C-W tree covers every rational number.
  (Infinite in two dimensions? No big deal, I can do that easily via diagonals; we just get lots of duplicates.)

  • C-W tree does not need diagonals, and never has duplicates.
    
    • ...I can't do that.
      • Apparently, I can't even understand the proof!

• Raku has rational numbers as a built-in type: Rat. Rat is auto-normalizing (3/6 becomes 1/2), has .numerator and .denominator methods, and a .nude method to get a list of both (Nu/De) at once.

• If you follow a fraction's C-W lineage all the way back to (but not including) the 1/1 root, reverse that lineage to be root-to-descendant, and map each fraction along-the-way as proper-fraction==L, improper-fraction==R (i.e. more than 1 or less than 1), then you get a navigation tree of which branch to follow, all the way to the original number. e.g. 8/19 has the navigation of RLRRLL.

  • To a percussionist, those navigations look just like snare drum rudiments and exercises: 'RLRRLL' is a single paradiddle-diddle
    • Those navigations can translate back-and-forth (if we are careful) to binary numbers, and so to plain decimal integers. (More on this when I discover the Curious Module below.)

• Exploring the tree via regular patterns of L(s) and R(s) finds some interesting properties:

  • 'LLLLLL'... and 'RRRRRR'... are the left and right edges of the tree, with top or bottom == 1.
    1/101 # 'L' x 100
    101/1 # 'R' x 100
  • R,'LLLLLL'... and L,'RRRRRR'... are the two center-most numbers ("framing" the half-way point) on any level after the first. Top or bottom will be '2'.
  • LR,'LLLLLL'... and LL,'RRRRRR'... frame the quarter-way point;
    RR,'LLLLLL'... and RL,'RRRRRR'... frame the three-quarter-way point on any level after the second. Top or bottom will be '3'.
  • (and so on, for row divisions by 8, 16, 32, ...)
  • Single-bit set (or unset) produce the top (or bottom) sequence 2,3,4...(size+1) as we slide the position of the bit:
    2/31 # RLLLLLLLLLLLLLLL
    3/44 # LRLLLLLLLLLLLLLL
    4/55 # LLRLLLLLLLLLLLLL
    ...
    31/2 # LRRRRRRRRRRRRRRR
    44/3 # RLRRRRRRRRRRRRRR
    55/4 # RRLRRRRRRRRRRRRR
  • Alternating L and R reaches the 1/3-point and 2/3-point in a row, producing approximations of the Golden Ratio φ ("The most irrational number"; 1.618033988749...), and its inverse|conjugate.
    These numbers are all ratios of successive Fibonacci numbers.
    e.g. LRLRLRLRLRLRLRLRLRL => 6765/10946 == F(20)/F(21) == 0.618034

After satisfying my urge for percussive exploration, I formalized the findings into a file of tests that the Perl and Raku solutions could both access, then wrote utility routines to help anyone who wants to explore more deeply.

I later found mention in a paper (URL?) that, unlike the Stern-Brocot tree, the C-W tree can be navigated directly across a row, also moving from the end of one row to the start of the next row. I added the calculation to the utility routines as `next-Calkin-Wilf-neighbor.

After all that, I found a Perl module on CPAN that solves the problem: Math::PlanePath::RationalsTree. This lead to a proof-of-concept one-liner, that calculates the parent but not the grandparent:

perl -MMath::PlanePath::RationalsTree -wE 'my $CW = Math::PlanePath::RationalsTree->new( tree_type => "CW" ); say join "/", $CW->n_to_xy( $CW->tree_n_parent( $CW->xy_to_n(@ARGV) ) );' 4817 5410

I cloned my original Perl solution and replaced my algorithm with calls to the module, as ch-2viamodule.pl, so I could be sure that the module could play in my drumming circle.

It worked perfectly, except where it didn't. Of 202 tests, only 166 passed.

Looking deeper into the 36 test failures, the problem became obvious. The module handles all types of rational trees with the efficient method of translating the LR navigation into zeros and ones to make (when decoded from binary) an integer. That integer represents the linear position of the rational.

$ perl -MMath::PlanePath::RationalsTree -wE 'my $CW = Math::PlanePath::RationalsTree->new( tree_type => "CW" ); say "N=$_ : tree_element=", join "/", $CW->n_to_xy( $_ ) for 1..5;'
N=1 : tree_element=1/1
N=2 : tree_element=1/2
N=3 : tree_element=2/1
N=4 : tree_element=1/3
N=5 : tree_element=3/2

The tree gets twice as big for every row (level?) you go down. Exponential growth! Around row 64, N will be around 2^64, and overflow the integer size of 64-bit Perl. All the tests below N=2^64 passed, as did some beyond that point (vagaries of rounding?), but you cannot rely on accuracy past that point. E.g.: finding the parent of "1/65" gives the wrong answer using the "convert to N" method, while 1/10001 and beyond all work with the direct calculations in Perl and Raku. (To be fair, Raku starts having problems past level 90 when drilling down along the Golden Ratio, due to Rat auto-collapsing into a more efficient Num. This could be prevented by using FatRat.)

Raku

Of note in my Raku solution :

• Clean separation of types: Calkin-Wilf-tree-parent() takes and returns Rat, and task2() takes and returns Str.
• Symmetry: task2() splits on slash at the start, and joins on slash at the end.
• Sequence: @lineage is a lazy Seq going all the way back to the root, generated by repeated calls to get the parent of the last result. This "keep feeding the result back in as the next argument" (iterated function) is a common-enough pattern that Raku directly supports it via the ... or "sequence" operator. Since the Seq is lazy, and we only ask for the first two ancestors (via .head), only two are calculated.
• Contain to Name: Placing the difference in its own variable allows not only DRY in the return statement, but also the symmetry between the two possible results. I particularly like how diff and -diff read, compared to n-d and d-n. (If I had not already committed, I might change diff/d to +diff/d to call attention the sign change).
• multi sub MAIN clearly shows the two ways to run the program.

Perl

Of note in my Perl solution :

• Clean separation of types: CalkinWilftree_parent() takes and returns a two-element [numerator,denominator] arrayref, and task2() takes and returns a "numerator/denominator" string.
• map==grep++ : map is also serving as grep via the empty-list trick; if no non-whitespace characters exist in the line, then map produces nothing for that line, not even undef; the line is skipped.
• /r : Using the r modifier (part of s{...}{...}msxr) on the substitution lets me return a changed copy, instead of modifying the original.

Kudos to manwar, and thanks to the whole team at The Weekly Challenge!

Elwood: What kind of music do you usually have here?
Claire: Oh, we got both kinds. We got Country and Western.

Rawhide!

These are some answers to the Week 146 of the Perl Weekly Challenge organized by Mohammad S. Anwar.

Spoiler Alert: This weekly challenge deadline is due in a few days from now (on January 9, 2022 at 24:00). This blog post offers some solutions to this challenge, please don’t read on if you intend to complete the challenge on your own.

Task 1: 10001st Prime Number

Write a script to generate the 10001st prime number.

10001st Prime Number in Raku

Raku has a fast is-prime subroutine or method, using the Miller-Rabin algorithm, to test whether a integer is prime. We can just generate an infinite (lazy) list of prime numbers and look for the 10000st one.

use v6;

my @primes = grep { .is-prime }, (1, 2, 3, -> $a { $a + 2} ...Inf);
say @primes[10001 - 1];  # Subtract 1 because the array starts at 0

This script displays the following output:

$ raku ./10001prime.raku
104743

The Raku script is so simple that it can be implemented as a short Raku one-liner:

$ ./raku -e 'say (grep { .is-prime }, 1..Inf)[10000]'
104743

10001st Prime Number in Perl

Since Perl doesn’t have a built-in is-prime subroutine, we implement our own. As finding the first 10001 primes is an intensive computation, we implement three performance optimizations compared to the naive brute-force solution: first, with the exception of 2, we only check odd integers. Second, we limit the tested divisors to the square root of the integer being checked. Finally, rather than testing all possible divisors, we test only the primes that we have already found. With these three optimizations, the script runs in less than 0.2 second, much faster than I expected.

use strict;
use warnings;
use feature "say";
use constant MAX => 10_001;

sub primes {
    my $max = shift;
    my @primes = (2, 3, 5);
    my $count = 3;
    my $candidate = $primes[-1];
    while ($count <= $max) {
        $candidate += 2;
        my $not_prime = 0;
        my $sq_cand = sqrt $candidate;
        for my $i (@primes) {
            $not_prime = 1, last unless $candidate % $i;
            last if $i > $sq_cand;
        }
        next if $not_prime;
        push @primes, $candidate;
        $count ++;
    }
    return $primes[$max-1];
}
my $p = primes(MAX);
say "$p";

This script displays the following output:

$ time perl ./10001prime.pl
104743

real    0m0,192s
user    0m0,124s
sys     0m0,077s

10001st Prime Number in Ring

I continue my exploration of Ring, a recent programming language (the first version was issued in 2016). The Ring implementation below is essentially a port of the Perl program above (with same performance optimizations):

p = primes(10001)
see p + nl

func primes max
    primes = [2, 3, 5]
    count = len(primes)
    candidate = primes[count]
    while count < max
        candidate += 2
        is_prime = True
        sqrt_cand = sqrt(candidate)
        for i in primes
            if candidate % i = 0
                is_prime = False
                exit
            ok
            if i > sqrt_cand exit ok
        next
        if is_prime 
            add(primes, candidate)
            count ++
        ok
    end
    return primes[max]

This program displays the following output:

$ ring ./10001prime.ring
104743

Note that Ring lists start with subscript 1, so we use index 10001 for finding the 10001 ptime number.

10001st Prime Number in Julia

function getprimes(max)
    primes = [2, 3, 5]
    count = 3
    candidate = 5
    while (count <= max)
        candidate += 2
        not_prime = false
        sq_cand = sqrt(candidate)
        for i in primes
            if (candidate % i == 0)
                not_prime = true
                break
            end
            i > max && break
        end
        not_prime && continue
        push!(primes, candidate)
        count += 1
    end
    return primes[max] # Julia arrays start with index 1
end

p = getprimes(10001)
println(p)

This program displays the following output:

$ julia 10001prime.jl
104743

Task 2: Curious Fraction Tree

Consider the following Curious Fraction Tree:

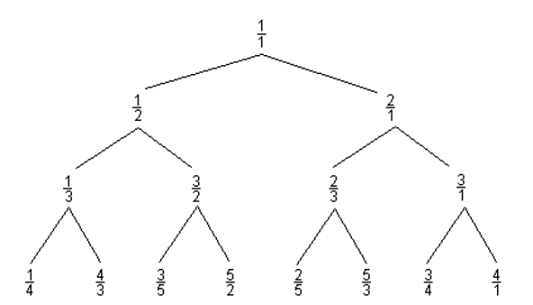
You are given a fraction, member of the tree created similar to the above sample.

Write a script to find out the parent and grandparent of the given member.

Example 1:

Input: $member = '3/5';
Output: parent = '3/2' and grandparent = '1/2'

Example 2:

Input: $member = '4/3';
Output: parent = '1/3' and grandparent = '1/2'

The first problem is to understand how this tree is constructed.

Each fraction has two children. It is easy to see that the left child is always a number smaller than 1 and the right child is always a number larger than 1. But how are the values generated?

Well, it is probably not so difficult to find out, but I must confess that I did not try very hard to find the constructing rules, but found them on the Curious Fraction Tree Web page. They are explained in this diagram:

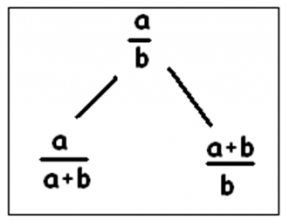
In other words, we have the following rules:

• For any node, the left child is less than 1 et the right child larger than 1;
• For node a/b, left child is a/(a+b) and right node is (a+b)/b.

From these two rules, it is easy to derive the reciprocal rules for finding the parent of a node:

• For a node x/y with a fraction less than 1, the parent is x/(y-x);
• For a node x/y with a fraction larger than 1, the parent is (x-y)/x.

It is now very easy to implement these rules in various programming languages.

There is, however, one little last problem. The task specifications do not tell us what to do about invalid input. For example, if the input is (1, 1) (the root to the tree), we will not be able to find a parent. Similarly, if we are given (1/2) as input, we will find (1, 1) as the parent, and will not be able to the grand-parent. We would have a problem if one of the values is 0. It is fairly easy to detect these problems, but I still wouldn’t know what to do about it. In many of the implementations below, I have decided that we must be given a valid input and will not try to validate the input. In some others, I have decided to detect some of these invalid input problems and tried to do something reasonable about them.

Curious Fraction Tree in Raku

We’re just implementing the rules above. Here, I do not try to validate the input.

Note that I was first tempted to implement the fraction as a Rat type of value, since it implements it as a numerator/denominator pair. I finally decided not to do that (because there may be some cases where the fraction might be reduced to their simplest form, division by 0 errors, and other such problems). So I decided to implement the fractions as integer pairs.

use v6;

# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x

sub parent (\num, \denom) {
    return num < denom ?? (num, denom - num) !! (num - denom, denom);
}
for (5, 2), (2, 5), (3, 4), (3, 5) -> $fraction {
    my $parent = parent |$fraction[0,1];
    my $gd-parent = parent |$parent[0,1];
    say "for child $fraction, parent is $parent and gd-parent is $gd-parent"; 
}

With the test fractions provided in the code, this program displays the following output:

raku ./fraction-tree.raku
for child 5 2, parent is 3 2 and gd-parent is 1 2
for child 2 5, parent is 2 3 and gd-parent is 2 1
for child 3 4, parent is 3 1 and gd-parent is 2 1
for child 3 5, parent is 3 2 and gd-parent is 1 2

Curious Fraction Tree in Perl

This program implements the rules described above. Here, we have made some effort to validate the input, just as an example: we write an error value if we get pas the root node.

use strict;
use warnings;
use feature "say";

# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x

sub parent {
    my ($num, $denom) = @{$_[0]};
    return ["Error"] if $num == $denom;
    return $num < $denom ? [$num, $denom - $num] : [$num - $denom, $denom];
}

for my $fraction ([5, 2], [2, 5], [3, 4], [3, 5], [2, 1], [1, 1]) {
    die "Invalid input node @$fraction" if $$fraction[0] == $$fraction[1];
    my $parent = parent $fraction;
    my $gd_parent = parent $parent;
    say "for child @$fraction, parent is @$parent and gd-parent is @$gd_parent"; 
}

This program displays the following output:

$ perl ./fraction-tree.pl
for child 5 2, parent is 3 2 and gd-parent is 1 2
for child 2 5, parent is 2 3 and gd-parent is 2 1
for child 3 4, parent is 3 1 and gd-parent is 2 1
for child 3 5, parent is 3 2 and gd-parent is 1 2
for child 2 1, parent is 1 1 and gd-parent is Error
Invalid input node 1 1 at fraction-tree.pl line 15.

Curious Fraction Tree in Some Other Programming Languages

In Ring

Again the same rules as before, with an attempt to handle gracefully some of the exceptions:

# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x

for test in [ [5, 2], [2, 5], [3, 4], [3,5], [6, 2], [1, 2] ]
    parent = find_parent(test[1], test[2])
    gd_parent = find_parent(parent[1], parent[2])
    see "Node " + to_str(test) + " has parent " + to_str(parent) + 
        " and grand-parent " + to_str(gd_parent) + nl
next

func find_parent num, denom
    if num < denom
        return [num, denom - num]
    but denom < num
        return [num - denom, denom]
    else 
        return ["Error", ""]
    ok

func to_str input
    return "" + input[1] + " " + input[2]

This script displays the following output:

$ ring ./fraction-tree.ring
Node 5 2 has parent 3 2 and grand-parent 1 2
Node 2 5 has parent 2 3 and grand-parent 2 1
Node 3 4 has parent 3 1 and grand-parent 2 1
Node 3 5 has parent 3 2 and grand-parent 1 2
Node 6 2 has parent 4 2 and grand-parent 2 2
Node 1 2 has parent 1 1 and grand-parent Error

In Python

No attempt here to validate the input.

# for a node x/y less than 1, parent is x/(y-x)
# for a node x/y larger than 1, parent is (x-y)/x

def find_parent(num, denom):
    return [num, denom - num] if num < denom else [num - denom, denom]

for test in ([5, 2], [2, 5], [3, 4], [3, 5]):
    parent = find_parent(test[0], test[1])
    gd_parent = find_parent(parent[0], parent[1])
    print("Node", test, "has parent", parent, "and grand-parent", gd_parent)

Output:

$ python3 ./fraction-tree.py
Node [5, 2] has parent [3, 2] and grand-parent [1, 2]
Node [2, 5] has parent [2, 3] and grand-parent [2, 1]
Node [3, 4] has parent [3, 1] and grand-parent [2, 1]
Node [3, 5] has parent [3, 2] and grand-parent [1, 2]

In Julia

Limited attempt to validate the input (catching only some of the exceptions).

function find_parent(num, denom)
    return num < denom ? [num, denom - num] :
           num > denom ? [num - denom, denom] :
           ("Error on node $num $denom");
end

for test in [ [5, 2], [2, 5], [3, 4], [3, 5], [1, 2] ]
    parent = find_parent(test[1], test[2])
    gd_parent = find_parent(parent[1], parent[2])
    println("Node $test has parent $parent and grand-parent $gd_parent")
end

Output:

# Node [5, 2] has parent [3, 2] and grand-parent [1, 2]
# Node [2, 5] has parent [2, 3] and grand-parent [2, 1]
# Node [3, 4] has parent [3, 1] and grand-parent [2, 1]
# Node [3, 5] has parent [3, 2] and grand-parent [1, 2]
# Node [1, 2] has parent [1, 1] and grand-parent Error on node

In Awk:

# Run for example as:
# echo ' 5/2
# 2/5
# 3/5' | awk -f fraction-tree.awk
function parent() 
{
    if (a < b) {
        b = b - a
    } else {
        a = a - b
    }
}
BEGIN {
    a = 0
    b = 0
    FS = "/"
}
{
    a = $1
    b = $2
    printf "Node = %d/%d: ", a, b
    parent()
    printf "Parent = %d/%d; ", a, b
    parent()
    printf "Grand-parent = %d/%d\n", a, b
}

Output:

$ echo ' 5/2
2/5
3/4
3/5
6/2 ' | awk -f fraction-tree.awk
Node = 5/2: Parent = 3/2; Grand-parent = 1/2
Node = 2/5: Parent = 2/3; Grand-parent = 2/1
Node = 3/4: Parent = 3/1; Grand-parent = 2/1
Node = 3/5: Parent = 3/2; Grand-parent = 1/2
Node = 6/2: Parent = 4/2; Grand-parent = 2/2

In Ruby

# For a node `x/y` with a fraction less than 1, the parent is `x/(y-x)`;
# For a node `x/y` with a fraction larger than 1, the parent is `(x-y)/x`.

def get_parent (pair)
    num = pair[0]
    denom = pair[1]
  return num < denom ? [num, denom - num] : [num - denom, denom];
end

tests = [ [5, 2], [2, 5], [3, 4], [3,5] ]
for test in tests
    parent = get_parent(test)
    gd_parent = get_parent(parent)
    print("Node #{test} - Parent: #{parent} - Grand-Parent: #{gd_parent}\n")
end

Output:

Node 5,2 - Parent: 3,2 - Grand-Parent: 1,2
Node 2,5 - Parent: 2,3 - Grand-Parent: 2,1
Node 3,4 - Parent: 3,1 - Grand-Parent: 2,1
Node 3,5 - Parent: 3,2 - Grand-Parent: 1,2

In Lua

-- For a node `x/y` with a fraction less than 1, the parent is `x/(y-x)`;
-- For a node `x/y` with a fraction larger than 1, the parent is `(x-y)/x`.

local function get_parent(pair)
    num = pair[1]
    denom = pair[2]
    -- no ternary operator in Lua, we can simulate it with and / or:
    return num < denom and {num, denom - num} or {num - denom, denom}
end

local function to_str(pair)
    -- return pair[1] .. "/" .. pair[2]
    return table.concat(pair, "/")
end

local tests = { {5, 2}, {2, 5}, {3, 4}, {3,5} }
for _, test in pairs(tests) do
    parent = get_parent(test)
    gd_parent = get_parent(parent)
    print("Node " .. to_str(test) .. " - Parent: " .. to_str(parent)
        .. " - Grand-Parent: " .. to_str(gd_parent))
end

Output:

$ lua ./fraction-tree.lua
Node 5/2 - Parent: 3/2 - Grand-Parent: 1/2
Node 2/5 - Parent: 2/3 - Grand-Parent: 2/1
Node 3/4 - Parent: 3/1 - Grand-Parent: 2/1
Node 3/5 - Parent: 3/2 - Grand-Parent: 1/2

In Kotlin

fun find_parent(pair: IntArray): IntArray {
    val num = pair[0]
    val denom = pair[1]
    return if (num < denom) intArrayOf(num, denom - num) else intArrayOf(num - denom, denom)
}

fun n2str (pair: IntArray): String {
    return "${pair[0]}/${pair[1]}"
}

fun main() {
val tests  = arrayOf(intArrayOf(5,2), intArrayOf(2,5), intArrayOf(3,4))
    for (test in tests) {
        val parent = find_parent(test)
        val gd_parent = find_parent(parent)
        print(n2str(test) + " - Parent: " + n2str(parent))
        println(" - Grand-parent: " + n2str(gd_parent))
    }
}

Output:

5/2 - Parent: 3/2 - Grand-parent: 1/2
2/5 - Parent: 2/3 - Grand-parent: 2/1
3/4 - Parent: 3/1 - Grand-parent: 2/1

In C

#include <STDIO>
void parent(int *a, int *b) {
    if (*a < *b) {
        *b -= *a;
    } else {
        *a -= *b;
    }
}

int main (void) {
    int num, denom;

    while (scanf ("%d/%d", &num, &denom) == 2) {
        printf("%d/%d - ", num, denom);
        parent(&num, &denom);
        printf("Parent: %d/%d - ", num, denom);
        parent(&num, &denom);
        printf("Grand-parent: %d/%d \n", num, denom); 
    }
    return (0);
}

Output:

$ echo ' 5/2
2/5
3/4
3/5' | ./a.out
5/2 - Parent: 3/2 - Grand-parent: 1/2
2/5 - Parent: 2/3 - Grand-parent: 2/1
3/4 - Parent: 3/1 - Grand-parent: 2/1
3/5 - Parent: 3/2 - Grand-parent: 1/2

In Scala

object fraction_tree extends App {

  def findParent(pair: List[Int]): List[Int] = {
    val num = pair(0)
    val denom = pair(1)
    return if (num < denom) List(num, denom - num) else List(num - denom, denom)
  }
  def n2str(pair: List[Int]): String = {
    return s"${pair(0)}" + "/" + s"${pair(1)}"
  }

  val tests: List[List[Int]] = List(List(5, 2), List(2, 5), List(3, 4))
  for (test <- tests) {
    val parent = findParent(test)
    val gd_parent = findParent(parent)
    println(n2str(test) + " - Parent: " + n2str(parent) + " - Grand-parent: " + n2str(gd_parent))
  }
}

Output:

5/2 - Parent: 3/2 - Grand-parent: 1/2
2/5 - Parent: 2/3 - Grand-parent: 2/1
3/4 - Parent: 3/1 - Grand-parent: 2/1

Wrapping up

The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on January 16, 2022. And, please, also spread the word about the Perl Weekly Challenge if you can.